3D Lingo

 III - Perspectives et faces cachées

Nous avons appris à déplacer un objet dans l'espace et même à modéliser des formes complexes. Mais il manque encore deux chose à notre animation. Un effet de perspective et des faces cachées

La perspective

Pour simuler la perspective nous allons mobiliser le troisième point de notre système de coordonnées 3D. Nous avons en effet tacitement résolu de confondre l'extrémité de l'axeZ est le lieu d'où la scËne est regardée. D'autres approches sont possibles. Notre option est seulement plus simple à mettre en œuvre. De toute façon, et quel que soit le procédé utilisé, le principe de la mise en perspective reste inchangé : Les transformations modifient la distance d'un point donné à l'observateur et plus cette distance est grande plus les objets semblent petit. Les points semblent même se confondre à l'infini, sur la ligne de fuite.

C'est en mesurant cette distance d'un point donné à l'observateur que nous seront en mesure de simuler un effet de perspective.

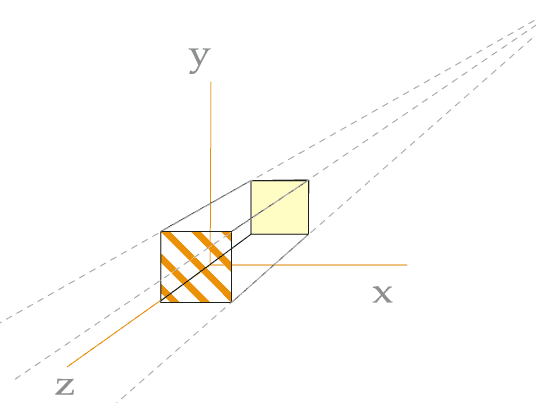
Reformulons ça dans notre langage : Les valeurs x et y d'un objet sont (paraissent) plus réduites (plus proches de zéro) à mesure de son éloignement (position sur l'axe z). Attention toutefois, cette modification est purement optique ne concerne que l'affichage des objets sur la scène de Director. En aucun cas, les coordonnées absolues des objets ne doivent être modifiées !

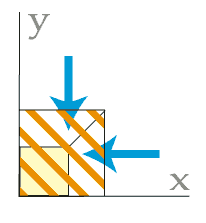
Nous allons modifier à l'affichage seulement, les positions horizontales et verticales de chaque coin des facettes et ce, en fonction de leur position sur l'axe Z. De notre animation, on reprend le behavior "facette" et plus particulièrement le gestionnaire "transformation" :

on transformation me, nouvellesCoordonnŽesDuSystemeLocal

LesQuad = []
if not pOk then exit
origineH = pPosition[1]
origineV = pPosition[2]

unCoin = equivalenceAbsolu (pc1[1] , pc1[2] , pc1[3], nouvellesCoordonnŽesDuSystemeLocal)
pc1 = unCoin

add LesQuad, point(unCoin[1] + origineH ,unCoin[2]+ origineV )
-- ajoute dans la liste "LesQuad" les deux premieres valeurs de pC1

unCoin = equivalenceAbsolu (pc2[1] , pc2[2] , pc2[3], nouvellesCoordonnŽesDuSystemeLocal)
pc2 = unCoin

add LesQuad, point(unCoin[1] + origineH ,unCoin[2] + origineV)

unCoin = equivalenceAbsolu (pc3[1] , pc3[2] , pc3[3], nouvellesCoordonnŽesDuSystemeLocal)
pc3 = unCoin

add LesQuad, point(unCoin[1] + origineH ,unCoin[2]+ origineV )

unCoin = equivalenceAbsolu (pc4[1] , pc4[2] , pc4[3], nouvellesCoordonnŽesDuSystemeLocal)
pc4 = unCoin

add LesQuad, point(unCoin[1] + origineH ,unCoin[2] + origineV)

the quad of sprite spriteNum = LesQuad

end

Dans ce gestionnaire les coordonnées des coins sont mémorisées par le sprite-facette dans des propriétés (pC1, pC2, pC3, pC4). La liste "lesQuad" utilise immédiatement les deux premières coordonnées de chaque coin afin de modifier les quads du sprite. Il nous faut certes CONSERVER les coordonnées absolues de pC1, pC2, etc. inchangées mais nous devons aussi infléchir les valeurs avant de les exploiter pour l'affichage. Nous nous dotons d'un gestionnaire supplémentaire qui diminue les coordonnée x et y en fonction de z pour un point donné :

on perspectiveDe unPoint
   x = integer(rho[1] * (1 - rho[3]/1000 ) )
  -- x est égale à zero si z = 1000 (c'est à dite au point de fuite)
  y = integer(rho[2] * (1 - rho[3]/1000 ) )
 -- y est égale à zero si z = 1000 (c'est à dite au point de fuite)
  z = rho[3]
 return [x, y , z]
end

NOTA : on peut en augmentant la valeur de division (ici 1000) créer un effet de distorsion ou de focale interessant. On pourrait par exemple en lieu et place de cette valeur de 1000, utiliser une variable globale que l'utilisateur serait libre d'incrémenter. Attention toutefois, les points éloignés au delà de cette limite risqueraient de se croiser à force de se rapprocher !

Nous modifions le gestionnaire "transformation" de façon à modifier À l'AFFICHAGE les coordonnées des coins :

on transformation me, nouvellesCoordonnŽesDuSystemeLocal

LesQuad = []
if not pOk then exit
origineH = pPosition[1]
origineV = pPosition[2]

unCoin = equivalenceAbsolu (pc1[1] , pc1[2] , pc1[3], nouvellesCoordonnŽesDuSystemeLocal)
pc1 = unCoin
-- NOTA : les nouvelles coordonnées absolues sont d'abord mémorisées dans pC1
-- ce sont les VRAIES coordonnées du coin
unCoin = perspectiveDe(unCoin)
add LesQuad, point(unCoin[1] + origineH ,unCoin[2]+ origineV )
-- on ajoute dans une liste les deux premières valeurs infléchies,
-- infléchies pour et seulement pour leur exploitation à l'affichage

unCoin = equivalenceAbsolu (pc2[1] , pc2[2] , pc2[3], nouvellesCoordonnŽesDuSystemeLocal)
pc2 = unCoin
unCoin = perspectiveDe(unCoin)
add LesQuad, point(unCoin[1] + origineH ,unCoin[2] + origineV)

unCoin = equivalenceAbsolu (pc3[1] , pc3[2] , pc3[3], nouvellesCoordonnŽesDuSystemeLocal)
pc3 = unCoin
unCoin = perspectiveDe(unCoin)
add LesQuad, point(unCoin[1] + origineH ,unCoin[2]+ origineV )

unCoin = equivalenceAbsolu (pc4[1] , pc4[2] , pc4[3], nouvellesCoordonnŽesDuSystemeLocal)
pc4 = unCoin
unCoin = perspectiveDe(unCoin)
add LesQuad, point(unCoin[1] + origineH ,unCoin[2] + origineV)

the quad of sprite spriteNum = LesQuad
-- la liste LesQuad contient donc les positions du sprite après rotation ET mise en perspective

end

Bien vu ! Rappelons-le toutefois ce n'est là qu'une des options possibles pour simuler la perspective. Notre choix n'est motivé que par la simplicité de mise en œuvre.

À y bien réfléchir, on épargnerait bien des efforts inutiles au processeur si l'on s'abstenait d'afficher les sprites trop éloignés. De même mais cette fois dans un souci de réalisme, il semblerait pertinent de ne pas afficher non plus les objets trop proches (comme s'ils étaient passés derrière le spectateur). On le voit, la position sur l'axe Z est sans cesse mobilisée pour construire un monde tri-dimensionnel. Mais laissons ces retouches accessoires car nous avons maintenant un problème beaucoup plus important. Que faire des faces cachées ?